Что называется решением неравенства с одной переменной что значит решить неравенство

wiki.eduVdom.com

Инструменты пользователя

Инструменты сайта

Боковая панель

Математика:

Контакты

Содержание

Неравенства с одной переменной и их системы

Общий способ сравнения чисел

Число а больше числа b (а>b), если их разность (а — b) — положительное число; число а меньше числа b, если их разность (а — b) — отрицательное число.

Свойства числовых неравенств:

Пример 1. Решите неравенства:
1.a) $\frac<4x-1> <2>— x > 3х + 2$
1.b) $\frac<4x-1> <2>— x \geq 3х + 2$..

Решение:

1.a	1.b
$\frac<4x-1> <2>— x > 3х + 2$.	$\frac<4x-1> <2>— x \geq 3х + 2$.
$$ \frac<4x-1> <2>— x > 3х + 2 \\ \frac<4x-1-2x> <2>> 3х + 2 \,\,\,\,|\cdot 2 \\ 2x-1 > 6x+4 \\ 2x-6x > 4+1 \\ -4x > 5 \,\,\,\,|:(-4) \\ -4 Ответы: 1.a) Ответ: $(-\infty;\;-\frac<5><4>)$ 1.b) Ответ: $(-\infty;\;-\frac<5><4>]$

Пример 2. Решите систему неравенств $$ \left\ <\begin(2x-3)-3(x-1)\geq 1 \\ 2(x+5)-x\leq 3 \end\right. $$

Решение: $$ \left\ <\begin(2x-3)-3(x-1)\geq 1 \\ 2(x+5)-x\leq 3 \end\right. \Leftrightarrow \left\ <\beginx\geq -1 \\ x\leq -7 \end\right. \text < - нет решений.>$$ Нельзя одновременно быть меньше -7 и больше -1.

Ответ: нет решений.

Пример 3. Решите неравенство $3x^2 — x — \frac<5> <4>\geq 0$.

Решение: Разложим квадратный трехчлен $3x^2 — x — \frac<5><4>$ на множители.

Для этого найдем его корни: $D = 1 + 4• 3• \frac<5> <4>= 16$;

$$ x = \frac<1\pm 4><6>; \\ x_1 = -\frac<1> <2>\\ x_2 = \frac<5> <6>\\ \\ 3x^2 — x — \frac<5> <4>= 3(x+\frac<1><2>)(x-\frac<5><6>) \\ 3x^2 — x — \frac<5> <4>\geq 0 \\ 3(x+\frac<1><2>)(x-\frac<5><6>)\geq 0 $$

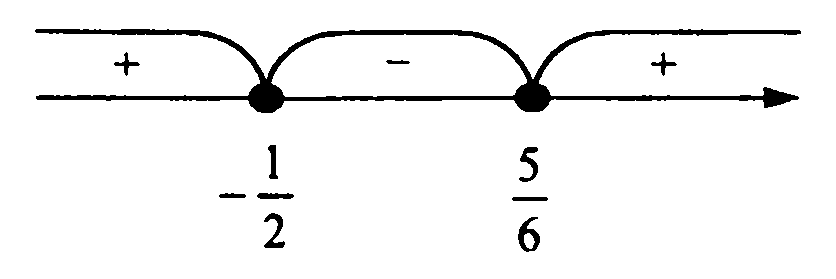
Пример 4. Решите неравенство $\frac\geq 0$.

Решение: $$ \frac\geq 0 \\ \\ \frac<(x-2)(x+2)>\geq 0 $$ Находим, что смена знака происходит, при $x = 0, \pm 1, \pm 2$. При этом помним, что $x \neq \pm 2$, поскольку тогда знаменатель обратиться в ноль, а делить на ноль нельзя.

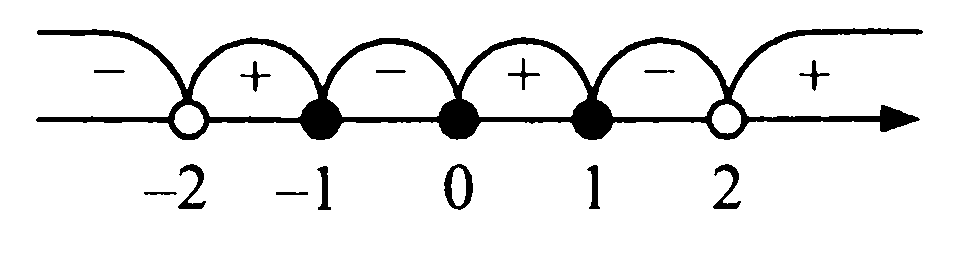
Пример 5. Под каким номером на каком рисунке верно указано решение системы неравенств? $$ \left\ <\begin5x+13 \leq 0 \\ x+5 \geq 1 \end\right. $$

Источник

Решение неравенств

Содержание:

Неравенство — это отношение, связывающее два числа или иных математических объекта с помощью одного из перечисленных ниже знаков.

Основные понятия, связанные с решением неравенств с одной переменной

Пусть дано неравенство f(x) > g(x). Всякое значение переменной х, при котором данное неравенство, обращается в верное числовое неравенство, называют решением неравенства. Решить неравенство с переменной — значит найти все его решения или доказать, что их нет.

Два неравенства с одной переменной называют равносильными, если решения этих неравенств совпадают; в частности, неравенства равносильны, если оба не имеют решений.

При решении неравенств обычно заменяют данное неравенство другим, более простым, но равносильным данному; полученное неравенство снова заменяют более простым, равносильным данному неравенством и т. д. Такие замены осуществляются на основе следующих утверждений.

Теорема 1.

Если из одной части неравенства перенести в другую слагаемое с противоположным знаком, то получится неравенство, равносильное данному.

Теорема 2.

Если обе части неравенства с одной переменной умножить или разделить на одно и то же положительное число, то получится неравенство, равносильное данному.

Теорема 3.

Если обе части неравенства с одной переменной умножить или разделить на одно и то же отрицательное число, изменив при этом знак неравенства на противоположный, то получится неравенство, равносильное данному.

Например, неравенства равносильны по теореме 1. Неравенства и равносильны по теореме 2 (обе части

неравенства разделили на положительное число 3, оставив без изменения знак -2 равносильны по теореме 3 (обе части неравенства —6х ).

На практике иногда полезны теоремы, являющиеся обобщениями теорем 2 и 3.

Теорема 4.

Если обе части неравенства умножить или разделить на одно и то же выражение, принимающее при всех значениях переменной положительные значения, то получится неравенство, равносильное данному.

Теорема 5.

Если обе части неравенства умножить или разделить на одно и то же выражение, принимающее при всех значениях переменной отрицательные значения, изменив при этом знак неравенства на противоположный, то получится неравенство, равносильное данному.

Графическое решение неравенств с одной переменной

Для графического решения неравенства f(x) > g(x) нужно построить графики функций у = f(x) и у = g(x) и выбрать те участки оси абсцисс, на которых график функции у = f(x) расположен выше графика функции у = g(x).

Пример:

Решить графически неравенство

Решение:

Построим в одной системе координат графики функций (рис. 1.113).

Из рисунка видно, что график функции расположен выше графика функции при х > 2.

Ответ:

Линейные неравенства с одной переменной

Линейным называют неравенство вида (или соответственно ). Если , то неравенство равносильно неравенству (см. теорему 2); значит, множество решений неравенства есть промежуток . Если , то неравенство равносильно неравенству (см. теорему 3); значит, множество решений неравенства есть промежуток . Если , то неравенство принимает вид ; оно не имеет решений, если , и верно при любых х, если b З и Зх-2 может быть и любой другой знак неравенства), где р(х) и q(x) — многочлены, основано на следующем рассуждении.

Рассмотрим выражение , где Если х > d, то каждый из множителей положителен и, следовательно, на промежутке имеем h(x) > 0. Если с 0 и т. д. (рис. 1.124).

Изменение знаков h(x) удобно иллюстрировать с помощью волнообразной кривой (ее называют «кривой знаков»), которую чертят справа налево, начиная сверху (рис. 1.125). Эту иллюстрацию нужно понимать так: на тех промежутках, где эта кривая проходит выше координатной прямой, выполняется неравенство h(x) > 0, на тех же промежутках, где кривая проходит ниже прямой, имеем h(x) g(x). В случае же, когда , неравенство равносильно неравенству противоположного смысла f(х) g(x). В случае же, когда , от исходного неравенства следует перейти к неравенству противоположного смысла f(х) 0 и g(x) > 0.

Таким образом, неравенство при равносильно системе неравенств

а при равносильно системе неравенств

Заметим, что систему (1) можно упростить: неравенство f(x) > 0 вытекает из неравенств f(x) > g(x), g(x) > 0, поэтому неравенство f(x) > 0 можно опустить, т. е. переписать систему (1) в виде

Аналогично, систему (2) можно переписать в виде

Пример 1.

Решить неравенство

Решение:

Так как , то данное неравенство можно переписать в виде Далее имеем

откуда

Пример 2.

Решить неравенство

Решение:

Чтобы все логарифмы имели смысл, должны выполняться неравенства х + 2 > 0 и 2х — 6 > 0. Используя свойства логарифмов, преобразуем заданное неравенство:

Таким образом, заданное неравенство равносильно системе неравенств

С помощью координатной прямой (рис. 1.128) устанавливаем, что множество решений последней системы, а значит, и заданного неравенства есть интервал (3; 8).

Иррациональные неравенства

При решении иррациональных неравенств используется следующее утверждение:

Теорема 8.

Если обе части неравенства принимают на некотором множестве X только неотрицательные значения, то, возведя обе части неравенства в квадрат (или в любую четную степень) и сохранив знак исходного неравенства, получим неравенство, равносильное данному (на множестве X).

Возведение обеих частей неравенства в одну и ту же нечетную степень (с сохранением знака неравенства) всегда является равносильным преобразованием неравенства.

Рассмотрим неравенство вида

(1)

Ясно, что решение этого неравенства является в то же время решением неравенства и решением неравенства g(x) > 0 (из неравенства (1) следует, что ). Значит, неравенство (1) равносильно системе неравенств

Так как при выполнении условий, задаваемых первыми двумя неравенствами этой системы, обе части третьего неравенства системы определены и принимают только неотрицательные значения, их возведение в квадрат есть равносильное преобразование неравенства. Выполнив это преобразование, придем к системе

Итак, неравенство равносильно системе неравенств

Рассмотрим теперь неравенство вида

(2)

Как и выше, заключаем, что , но в отличие от предыдущего случая здесь g(x) может принимать как неотрицательные, так и отрицательные значения. Поэтому заданное неравенство (2) рассмотрим в каждом из следующих случаев: g(x) 0.

Решение:

Построим график функции у = sin х и выберем на оси х значения аргумента х, которым соответствуют точки графика, лежащие выше оси х. Одним из промежутков, содержащих такие точки оси х, является интервал (рис. 1.129), а всего таких интервалов будет бесконечно много,

причем в силу периодичности функции у = sin х каждый из них получается из сдвигом по оси х на Таким образом, решением заданного неравенства служит объединение интервалов вида Это можно записать так:

Пример 2.

Решить неравенство

Решение:

Построим график функции у = cos х и проведем прямую Нас интересуют те значения аргумента х, которым соответствуют точки графика, лежащие ниже прямой Одним из нужных нам промежутков является интервал (рис. 1.130).

Воспользовавшись периодичностью функции у = cos х, запишем ответ:

Пример 3.

Решить неравенство .

Решение:

Построим график функции у = tg х и проведем прямую у = -1. Нас интересуют те значения х, которым соответствуют точки графика, лежащие не ниже прямой у = — 1.

Одним из нужных нам промежутков является (рис. 1.131), а всего таких промежутков будет бесконечно много, причем в силу периодичности функции у = tg х каждый получается из сдвигом по оси х на Это позволяет записать решение следующим образом:

Неравенства и системы неравенств с двумя переменными

Рассмотрим неравенство f(x; у) > g(x; у). Решением неравенства с двумя переменными называют пару значений переменных, которая обращает неравенство с переменными в верное числовое неравенство. Известно, что пара действительных чисел (х; у) однозначно определяет точку координатной плоскости. Это дает возможность изобразить решения неравенства или системы неравенств с двумя переменными геометрически, в виде некоторого множества точек координатной плоскости.

Пример 1.

Изобразить на координатной плоскости множество решений неравенства х + у — 1 > 0.

Решение:

Преобразуем данное неравенство к виду у > -х + 1. Построим на координатной плоскости прямую у = -х + 1. Так как ордината любой точки, лежащей выше прямой у = —х + 1, больше, чем ордината точки, имеющей такую же абсциссу, но лежащей на прямой, то множество точек плоскости, расположенных выше этой прямой, и будет геометрическим изображением решений заданного неравенства (рис. 1.132).

Пример 2.

Изобразить на координатной плоскости множество решений неравенства

Решение:

Преобразуем неравенство к виду . Построим на координатной плоскости параболу — график функции .

Так как ордината любой точки, лежащей выше параболы , больше, чем ордината точки, имеющей ту же абсциссу, но лежащей на параболе, и так как неравенство нестрогое, то геометрическим изображением решений заданного неравенства будет множество точек плоскости, лежащих на параболе и выше нее (рис. 1.133).

Пример 3.

Изобразить на координатной плоскости множество решений системы неравенств

Геометрическим изображением решений системы неравенств является множество точек первого координатного угла (рис. 1.134). Геометрическим изображением решений неравенства х + у 4 или, поскольку х > 0, неравенства является множество точек, лежащих выше ветви гиперболы, служащей графиком функции (рис. 1.136). В итоге получаем множество точек координатной плоскости, лежащих в первом координатном углу ниже прямой, служащей графиком функции у = 5 — х, и выше гиперболы, служащей графиком функции (рис. 1.137).

Эта лекция взята со страницы полного курса лекций по изучению предмета «Математика»:

Смотрите также дополнительные лекции по предмету «Математика»:

Неравенства и их геометрическое содержание

Метод координат позволяет геометрически толковать не только уравнения, а так же и неравенства.

Потому как мы говорим, что уравнение с двумя переменными и обозначает на плоскости некоторую линию, можно сказать, что неравенство с двумя переменными и обозначается множество точек плоскости, координаты которых удовлетворяют этому неравенству. Таким образом геометрически толковать и неравенство

Если выражение является линейным, то есть где — постоянные, то мы получим линейное уравнение

и два линейные неравенства

Если коэффициенты и не равны одновременно нулю, то уравнение (2.40) обозначает на плоскости прямую, а неравенства (2.41) и (2.42) — соответственно две полуплоскости, на которой прямая (2.40) разбивает координатную плоскость. Для того чтобы выяснить, какая из двух полуплоскостей обозначается заданной линейным неравенством, можно использовать, например, такой способ.

Выберем какую нибудь точку. подставим ее координаты в неравенство, что проверяется.

Если координаты точки удовлетворяют неравенству, то неравенство обозначает ту плоскость, в которой находится выбранная точка: если же координаты точки не удовлетворяют неравенство, то неравенство обозначает плоскость, которая не содержит выбранной точки.

Пример:

Записать с помощью неравенства ту полуплоскость, в которой лежит точка и границей которой прямая Проверить, лежит в этой же полуплоскости начало координат.

Решение. Подставим координаты точки в левую часть уравнения заданной прямой: Полученная величина положительна. Следует, точка не принадлежит на заданной прямой, а искомая плоскость обозначается неравенством

Студенту рекомендовано сделать рисунок и решить самостоятельно вторую часть примера.

Можно рассмотреть также систему неравенств:

Областью решения системы неравенств называется множество всех точек, координаты каждой из них удовлетворяют всем неравенствам системы.

пересечением нескольких множеств точек называется множество точек, каждая из которых принадлежим всем множествам, что пересекаются. Очевидно, областью решения системы неравенства служит пересечение областей решения каждой из неравенства системы.

Областью решений, системы линейных уравнений

является, очевидно пересечение полуплоскостей, что обозначается каждой из неравенств системы. Эта область может быть и пустым множеством, то есть множеством, которая не содержит ни одной точки.

Если же это множество точек не пустое, то она обозначается многоугольной областью. Если кроме того, эта область ограничена, то есть не содержит точек как и при большим значением координат, то ее называют началом многоугольника.

Пример:

Записать с помощью системы неравенств множество точек, что лежат посередине треугольника с вершинами

Решение. Студенту рекомендовано выполнить рис., очевидно, множество всех внутренних точек треугольника можно рассмотреть как пересечение трех полуплоскостей, из которых первая ограничена прямой и содержит точку вторая ограничена прямой и содержит точку

найдем неравенство, что обозначает первую из этих полуплоскостей. Сложим уравнение прямой зная координаты точек и

или

Подставляя в левую часть этого уравнения координаты точки получим Следует, первая полуплоскость обозначается неравенством

Аналогично, плоскость, что ограничена прямой и содержит точку обозначается неравенством:

А плоскость, что ограничена прямой и содержит точку обозначается неравенством:

Следует множество всех внутренних точек треугольника обозначается системой неравенств

Если вместо строгих неравенств ( или ) рассматривать не строгие неравенства ( или ), то обозначенная ими область включается и границы этих полуплоскостей.

Например, область решений неравенств:

является область, что ограничена треугольником включая ее как внутренние, так и граничные точки, то есть и точки отрезков

Аналогично интерпретируются геометрически линейные неравенства тремя переменными. Линейное неравенство с тремя неизвестными обозначается полуплоскость, а система таких неравенств — пересечение полупространства. Если он не пустой, является многогранной областью или в случае ограниченности многогранником.

Примеры решения задач:

Задача 2.121.

Построить область решений системы линейных неравенств:

Решение. Построим граничные прямые, что соответствуют данным неравенств, по двум точкам, что соответствуют этим прямым

Каждая прямая делит плоскость на две полуплоскости. Та из них, что содержит начало координат и является областью решений каждой из неравенств. Стрелками обозначим полуплоскости, которые являются областями решений данных неравенств. Пересечение отмеченных полуплоскостей — четырехугольник — область решения данной системы (рис. 2.21).

Задача 2.122 Построить область решений системы линейных неравенств:

Решение. Построим граничные прямые, что соответствуют данным неравенствам:

Область решение первой прямой содержит начало координат, а область решений второй и третьей неравенств — не содержат начало координат. Стрелками обозначим полуплоскости, точки которых удовлетворяют неравенствам. Областью решений является выпуклая неограниченная область (рис. 2.22).

Задача 2.123

Построить область решений системы линейных неравенств:

Решение. Строим граничные прямые:

Строим область решений каждого неравенства (рис. 2.23).

Не существует ни одной точки для всех плоскостей, что соответствуют данным уравнениям. Следует, область решений пустая. Система неравенств несовместима.

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

Источник