Аппроксимировать что это значит

Что такое аппроксимация

Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Многие термины, используемые точными науками, находят свое применение и в обыденной жизни.

Сегодня рассмотрим один из них, термин «аппроксимация».

Узнаем, что такое аппроксимация в математике и в каких ситуациях это понятие можно использовать, исключая точные науки.

Аппроксимация в математике — это …

Как правило, суть термина раскрывается, если его перевести на родной язык. В переводе с латинского «proxima» – это «ближайшая», более широкое толкование перевода – «приближение».

Следовательно, аппроксимация – это метод вычислений, используемый в математике, заключающийся в том, что сложные математические объекты при расчетах (других исследованиях) заменяются более простыми (но максимально похожими).

Пример: при расчетах, в которых используются иррациональные числа (бесконечные десятичные дроби), эти числа заменяются рациональными числами (конечными дробями), приближенными по количественному значению. Этот метод называется диофантовым приближением и является примером применение метода аппроксимации.

Знакомое нам всем число π (пи) – это бесконечная десятичная дробь. π = 3,1415926535897932 …. При вычислениях, в которых используется число «пи», принято брать не дробь целиком (но это и невозможно, ведь она бесконечна), а только 2 цифры после запятой.

Таким образом, принято считать, что π = 3,14. И это тоже применение метода аппроксимации.

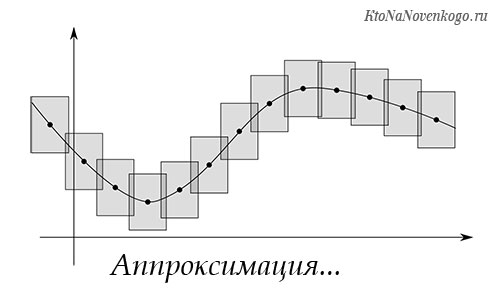
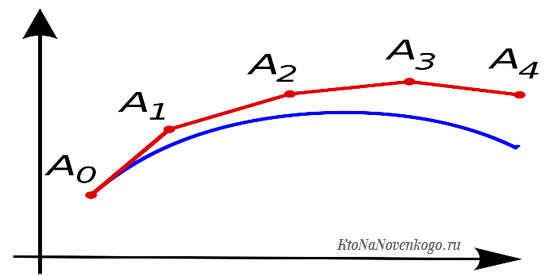
В геометрии метод аппроксимации используется в действиях с кривыми: для удобства вычислений они заменяются ломаными. Как это выглядит, можно посмотреть на схеме:

Кривая (синий цвет) для проведения каких-либо вычислений аппроксимируется в ломаную, каждое из звеньев которой имеет вершины с координатами, максимально приближенными к координатам кривой.

Термин «аппроксимация» схож по сути со следующими математическими понятиями:

1. подобие;
2. округление;
3. равновеликость;
4. среднее значение.

Применение термина «аппроксимация» в иных областях

Суть термина применительно к философским категориям остается той же, что и в математике – это указание на приблизительный характер какого-либо процесса, явления.

Аппроксимация в экономике – это метод, используемый в моделировании экономических ситуаций, а именно – замена сложных производственных или иных экономических объектов более простыми (при сохранении основных входных и выходных параметров этих объектов).

Данный метод позволяет решать сложные задачи с помощью «пожертвования» деталями, что делает алгоритм решения (это что?) более простым.

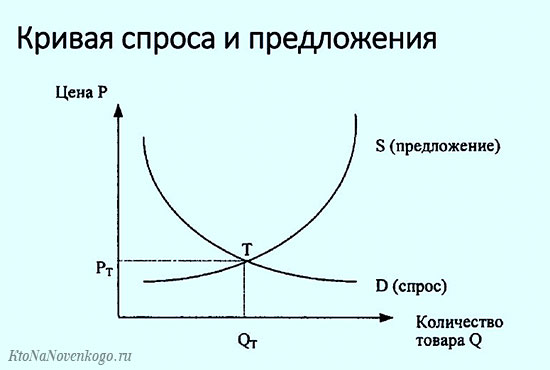
Приведу простой пример: для построения кривых спроса (что это?) и предложения используются показатели цены и количества проданных товаров. Это наглядно изображено на рисунке ниже:

На самом деле на спрос и предложение влияние оказывают и другие факторы.

При проведении анализа эти факторы не учитывают, принимая во внимание только цену и проданный товар, следовательно, построенные кривые являются аппроксимацией более сложных кривых. Но для оценки данной экономической ситуации полученные аппроксимированные графики являются достаточными.

Аппроксимация в повседневной жизни – это обобщение ряда событий, имеющих одинаковый посыл. Например, на вопрос: «Как дела?», мы чаще всего отвечаем: «Нормально, все в порядке».

Это аппроксимация оценки своей жизни, своей деятельности за недавний отрезок времени. На самом деле происходило и плохое, и хорошее, но в целом – «все по среднему», мы не вдаемся в подробности и не рассказываем, что произошло за, допустим, последнюю неделю.

Или еще пример: вчера весь день светило солнце, несколько раз «занавешиваясь» облачками. Но на вопрос о погоде мы ответим, что было солнечно, и не будем рассказывать о ее небольших изменениях, потому что они были недолгими, и не существенными.

Краткое резюме

Мы рассмотрели применение термина «аппроксимация» в различных областях. Следует отметить, что практическое использование аппроксимации в алгебре и геометрии очень специфично, поэтому в этой статье детального разъяснения нет.

Для тех, кто хочет подробней узнать про аппроксимацию функций привожу 2 ссылки: первая – лекция общего характера, другая – монография по этой же теме с прикладным уклоном.

Читайте наш блог, это познавательно!

Автор статьи: Елена Копейкина

Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru

Эта статья относится к рубрикам:

Комментарии и отзывы (2)

Мне думается, математики, социологи, маркетологи и проч. знают этот термин. Всем же прочим просто не нужно такое специфическое слово. Ну как его использовать вне профессиональной сферы?

Происхождение этого слова я вижу от английского «approximately», что означает «приблизительно». Оно в свою очередь от другого слова, кстати очень распространенный термин в авиации — «approach», то есть приближение, подход.

Источник

Значение слова «аппроксимация»

• Аппроксима́ция (от лат. proxima – ближайшая) или приближе́ние — научный метод, состоящий в замене одних объектов другими, в каком-то смысле близкими к исходным, но более простыми.

Аппроксимация позволяет исследовать числовые характеристики и качественные свойства объекта, сводя задачу к изучению более простых или более удобных объектов (например, таких, характеристики которых легко вычисляются или свойства которых уже известны). В теории чисел изучаются диофантовы приближения, в частности, приближения иррациональных чисел рациональными. В геометрии рассматриваются аппроксимации кривых ломаными. Некоторые разделы математики в сущности целиком посвящены аппроксимации, например, теория приближения функций, численные методы анализа.

В переносном смысле употребляется в философии как метод приближения, указание на приблизительный, неокончательный характер. Например, в таком смысле термин «аппроксимация» активно употреблялся Сёреном Кьеркегором (1813—1855) в «Заключительном ненаучном послесловии…»

аппроксима́ция

1. матем. приближённое выражение некоторых величин или объектов через другие, более простые величины или объекты ◆ Вследствие того, что массы элементарных частиц распределены в пределах многих порядков, аппроксимацию распределения целесообразно представить в логарифмическом масштабе. Воспоминания о Шкловском, «1996» (цитата из НКРЯ) ◆ Коэффициент аппроксимации 6,8% свидетельствует о высокой степени согласия уравнения регрессии с фактическими величинами. «Прогноз необходимости борьбы с непарным шелкопрядом в нагорных дубравах», 2004 г. // «Лесное хозяйство» (цитата из НКРЯ)

2. перен. филос. метод приближения, указание на приблизительный, неокончательный характер чего-либо

Фразеологизмы и устойчивые сочетания

Делаем Карту слов лучше вместе

Привет! Меня зовут Лампобот, я компьютерная программа, которая помогает делать Карту слов. Я отлично умею считать, но пока плохо понимаю, как устроен ваш мир. Помоги мне разобраться!

Спасибо! Я стал чуточку лучше понимать мир эмоций.

Вопрос: пустомеля — это что-то нейтральное, положительное или отрицательное?

Источник

Аппроксимация

Аппроксима́ция, или приближе́ние — научный метод, состоящий в замене одних объектов другими, в том или ином смысле близкими к исходным, но более простыми.

Аппроксимация позволяет исследовать числовые характеристики и качественные свойства объекта, сводя задачу к изучению более простых или более удобных объектов (например, таких, характеристики которых легко вычисляются, или свойства которых уже известны). В теории чисел изучаются диофантовы приближения, в частности, приближения иррациональных чисел рациональными. В геометрии рассматриваются аппроксимации кривых ломаными. Некоторые разделы математики в сущности целиком посвящены аппроксимации, например, теория приближения функций, численные методы анализа.

В переносном смысле употребляется в философии как метод приближения, указание на приблизительный, неокончательный характер. Например, в таком смысле термин «аппроксимация» активно употреблялся Сёреном Кьеркегором (1813—1855) в «Заключительном ненаучном послесловии…»

Примеры

В этом разделе не хватает ссылок на источники информации.

• Для приближенного вычисления интеграла используется формула прямоугольников или формула трапеций, или более сложная квадратурная формула. Фактически при этом происходит приближение подинтегральной функции ступенчатой функцией или вписанной ломаной, интеграл от которой считается мгновенно.
• Для вычисления значений сложных функций часто используется вычисление значения отрезка ряда, аппроксимирующего функцию.
• Для обработки экспериментальных или натурных данных. Тут следует рассматривать два случая: 1) аппроксимирующая функция ограничена диапазоном заданных точек и служит в качестве только интерполирующей зависимости; 2) аппроксимирующая функция выступает в роли физического закона и с ее помощью допускается экстраполировать переменные. Приведем пример. Пусть на основе натурных наблюдений получены следующие пары чисел x и y (см. [1]):

Если функция будет использована только для интерполяции, то достаточно аппроксимировать точки полиномом, скажем, пятой степени:

Намного сложней обстоит дело в случае, если приведенные выше натурные данные служат опорными точками для выявления закона изменения y=F(x) с известными граничными условиями. Например: F(0)=0 и . Тут уже качество результата зависит от профессионализма исследователя. В данном случае наиболее приемлемым окажется закон:

Для оптимального подбора параметров уравнений обычно используют метод среднеквадратичных отклонений .

См. также

Ссылки

Wikimedia Foundation . 2010 .

Полезное

Смотреть что такое «Аппроксимация» в других словарях:

АППРОКСИМАЦИЯ — АППРОКСИМАЦИЯ (от лат. approximare приближаться) метод сознательного упрощения “слишком точного” теоретического знания с целью привести его в соответствие с потребностями и возможностями практики. Напр., использование числа π с точностью до… … Философская энциклопедия

Аппроксимация — (approximation приближение) процедура выбора оптимальной аппроксимирующей функции из определенного класса функций. Следует различать параметрическую и непараметрическую аппроксимацию. При параметрической аппроксимации общий вид (формула, модель)… … Официальная терминология

АППРОКСИМАЦИЯ — [ Словарь иностранных слов русского языка

аппроксимация — приближение; апроксимирование, апроксимация, линеаризация Словарь русских синонимов. аппроксимация сущ., кол во синонимов: 3 • апроксимация (2) • … Словарь синонимов

аппроксимация — и, ж. approximation, нем. Approximation <лат. approximare приближаться. мат. Приближенное выражение каких л. величин через другие, более простые величины. Крысин 1998. | Аппроксимация называется официальное снижение требований в школьной… … Исторический словарь галлицизмов русского языка

Аппроксимация — приближенное решение сложной функции с помощью более простых, что резко ускоряет и упрощает решение задач. В экономике целью А. часто является укрупнение характеристик моделируемых экономических объектов. Словарь бизнес терминов. Академик.ру.… … Словарь бизнес-терминов

АППРОКСИМАЦИЯ — (от лат. approximo приближаюсь) замена одних математических объектов (напр., чисел или функций) другими, более простыми и в том или ином смысле близкими к исходным (напр., кривых линий близкими к ним ломаными) … Большой Энциклопедический словарь

АППРОКСИМАЦИЯ — приближенное выражение математических величин (чисел, функций и т. п.) через другие. Любую непрерывную функцию f(x), a ≤ х ≤ b можно аппроксимировать алгебраическими или тригонометрическими многочленами. Важно определить степень… … Геологическая энциклопедия

АППРОКСИМАЦИЯ — (от лат. approximare – приближаться). Обучение иноязычному произношению, ограниченное приближением к правильному произношению и допускающее «снисходительное отношение» к фонетическим ошибкам, не нарушающим коммуникацию. Однако А. не должна… … Новый словарь методических терминов и понятий (теория и практика обучения языкам)

Аппроксимация — [approximation] «замена одних математических объектов другими, в том или ином смысле близкими к исходным»[1] ; в частности приближенное выражение сложной функции с помощью более простых. Например, при кусочно линейной А., непрерывная… … Экономико-математический словарь

аппроксимация — «Замена одних математических объектов другими, в том или ином смысле близкими к исходным» [1]. В частности — приближенное выражение сложной функции с помощью более простых. Например, при кусочно линейной А., непрерывная… … Справочник технического переводчика

Источник